Transfert en cours..., vous êtes sur le "nouveau" serveur data.abuledu.org dont l'hébergement est financé par l'association abuledu-fr.org grâce à vos dons et adhésions !
Vous pouvez continuer à soutenir l'association des utilisateurs d'AbulÉdu (abuledu-fr.org) ou l'association ABUL.
Suivez la progression de nos travaux et participez à la communauté via la liste de diffusion.
Votre recherche ...
Nuage de mots clés
Dessins et plans, Jeux mathématiques, Cercles, Géométrie des cercles, Mathématiques récréatives, Théodore Motzkin (1908-1970)
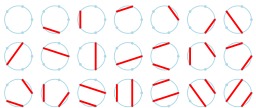
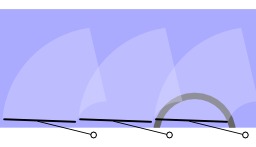
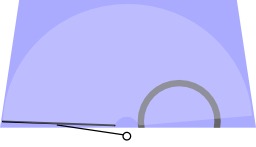
Cordes de Motzkin entre cinq points sur un cercle
Vingt-une cordes de Motzkin (qui ne se coupent pas) entre cinq points sur un cercle.
Dessins et plans, Jeux mathématiques, Cercles, Géométrie des cercles, Mathématiques récréatives, Théodore Motzkin (1908-1970)
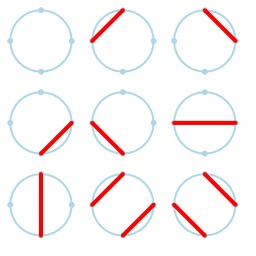
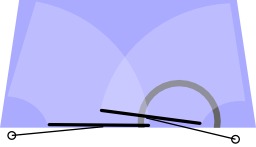
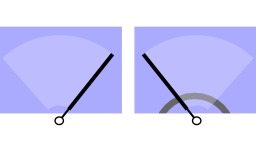
Cordes de Motzkin entre quatre points sur un cercle
Cordes de Motzkin sur un cercle : les neuf manières de dessiner des cordes qui ne se coupent pas entre quatre points d'un cercle. Le nombre de Motzkin est le nombre de façons de choisir des cordes ne se coupant pas, parmi les cordes reliant n points disposés sur un cercle. Source : http://fr.wikipedia.org/wiki/Nombre_de_Motzkin.
Dessins et plans, Géométrie, Compas, Dessin -- Matériel, Arcs, Dessin -- Instruments, Constructions géométriques, Cercles, Dessin -- Technique, Constructions à la règle et au compas
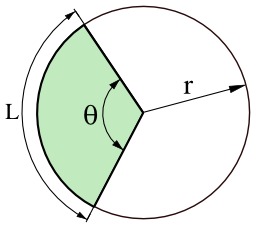
Arc de cercle
Cercle de rayon "r", arc de cercle de longueur "L" soustendu par un angle θ (theta) avec un secteur circulaire de surface "A".
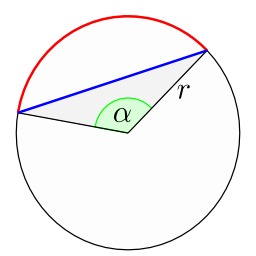
Arc et corde d'un cercle
Un cercle est une courbe plane fermée constituée des points situés à égale distance d'un point nommé centre. La valeur de cette distance est appelée rayon du cercle. Une corde (en bleu) est un segment de droite dont les extrémités se trouvent sur le cercle. Un arc est une portion de cercle délimitée par deux points (en rouge). Un secteur circulaire est une partie du disque comprise entre deux rayons. Un angle au centre (vert) est un angle formé par deux rayons du cercle.
Dessins et plans, Cercles, Polygones, Aires (surfaces), Aires (surfaces) -- Mesure, Géométrie des nombres, Nombres non-rationnels, Nombres transcendants, Pi (le nombre)
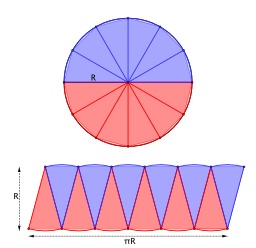
Calcul de l'aire du cercle avec Géogébra
Calcul de l'aire du cercle avec Géogébra : rayon x demi-circonférence. On déduit d’une propriété analogue pour les polygones réguliers que l’aire d’un cercle égale son demi-périmètre multiplié par son rayon. le périmètre du polygone est à peu près 2πr alors qu’en redistribuant les triangles formés on remarque que son aire est à peu près πr2. Pour formaliser le « à peu près » il faudrait faire tendre le nombre de côtés du polygone vers l’infini, ce qui illustre déjà la nature « analytique » de π.
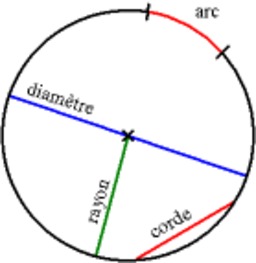
Cercle et son vocabulaire
Définition des termes géométriques concernant le cercle : arc, rayon, diamètre, corde.
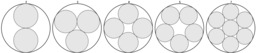
Cercles dans un cercle
Schéma des configurations de 5 cercles avec respectivement 2, 3, 4, 5 et 7 cercles inscrits.
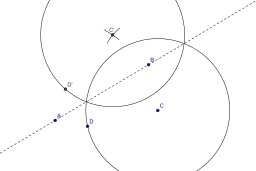
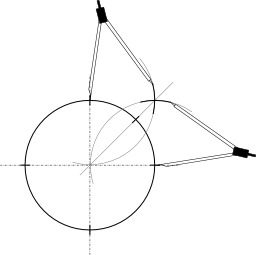
Construction au compas de l'intersection d'une droite et d'un cercle
Construction au compas seul de l'intersection d'une droite et d'un cercle (cas général) : Si la droite (AB) n'est pas un diamètre du cercle, il suffit de construire le symétrique du cercle par rapport à la droite (AB). Les points d'intersection des deux cercles sont aussi les points d'intersection du cercle de départ avec la droite (AB).
Dessins et plans, Géométrie, Compas, Parallèles (géométrie), Constructions géométriques, Milieux (géométrie), Segments (géométrie)
Construction au compas du milieu d'un segment
Construction au compas seul du milieu d'un segment : Le point A' est le symétrique de A par rapport à B. Les cercles de centre A' passant par A et de centre A passant par B se rencontrent en C et D. Le point D' est le symétrique de D par rapport à A. I est le quatrième point du parallélogramme AD'CI.
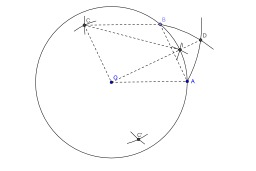
Construction d'un parallélogramme au compas
Construction au compas seul du quatrième point d'un parallélogramme : Les points A, B et C étant donnés, le quatrième point D du parallélogramme ABCD est le point d'intersection du cercle de centre A et de rayon BC et du cercle de centre C et de rayon BA non situé dans le demi-plan de frontière (CA) contenant B.
Construction du milieu d'un arc au compas
Construction au compas seul du milieu d'un arc : OABC est un parallélogramme de la forme OA=OB, I est le milieu de l'arc AB de centre O, D est le point de la demi-droite [OI) telle que CA=CD, alors OD=CI. En effet, CD^2=CA^2=2CO^2+OA^2. Ensuite il suffit d'appliquer le théorème de Pythagore dans les deux triangles rectangle COI et COD : CI^2=CO^2+OI^2=CO^2+OA^2, OD^2=CD^2-CO^2=CO^2+OA^2. Or cette figure est réalisable au compas seul et permet donc de placer le point I. Si l'on suppose donnés le point O et l'arc AB, on construit le point C intersection du cercle de centre B et passant par A avec le cercle de centre O et de rayon AB. On construit de même le point C' intersection du cercle de centre A passant par O et du cercle de centre O et de rayon AB. Le point D est à l'intersection des cercles de centre C et C' et passant par A et B. Le point I est à l'intersection des cercles de centre C et C' et de rayon OD.
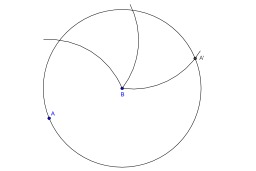
Construction du Symétrique d'un point au compas
Construction au compas seul du symétrique d'un point par rapport à un point : Le symétrique du point A par rapport au point B est le point situé sur le cercle de centre B et passant par A et diamétralement opposé à A. Il se construit en reportant trois fois le rayon sur le cercle.
Dessins et plans, Géométrie, Drapeaux, Douze (le nombre), Pays de l'Union européenne, Histoire, Europe
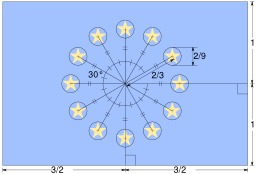
Construction géométrique du drapeau de l'Europe
Construction géométrique du drapeau de l'Europe : Le drapeau est rectangulaire avec une proportion de 2:3. Il est composé d'un cercle de douze étoiles d'or sur un champ d'azur. Toutes les étoiles sont disposées verticalement (la pointe vers le haut), ont cinq branches et sont espacées de façon égale selon les positions des heures sur cadran d'une horloge. Chaque rayon d'étoile est égal à un dix-huitième de la hauteur du guindant. La description héraldique officielle donnée par l'Union européenne est : « Le drapeau européen est représenté par un cercle de douze étoiles d'or sur fond bleu. Les étoiles symbolisent les idéaux d'unité, de solidarité et d'harmonie entre les peuples d'Europe. »
Dessins et plans, Géométrie, Compas, Dessin -- Matériel, Arcs, Dessin -- Instruments, Constructions géométriques, Cercles, Dessin -- Technique, Constructions à la règle et au compas, Compas,
Couper un cercle en 8
Le tracé d'une bissectrice permet de définir deux arcs égaux, et ici de diviser le cercle en 8 parties égales : placer un point entre chaque point déjà placé : on place la pointe du compas sur un des points et l'on trace un arc de cercle à l'extérieur du cercle de base, et l'on fait de même sur le point voisin ; l'intersection des deux arcs définit un point. Puis, on trace à la règle le diamètre passant par ce point-là ; il coupe l'arc de cercle en deux parts égales (bissectrice de l'angle). Ainsi, si le cercle est déjà coupé en 4 parts, on en obtient 8 ; si le cercle est déjà coupé en 12 parts, on en obtient 24. On peut recouper les arcs en 2 par la même méthode, et multiplier ainsi le nombre d'arcs par 2, pour obtenir encore plus d'arcs.
Dessins et plans, Géométrie, Compas, Dessin -- Matériel, Dessin -- Instruments, Constructions géométriques, Cercles, Dessin -- Technique, Constructions à la règle et au compas
Couper un cercle en douze parties égales
Méthode pour couper un cercle en douze parties égales en trois étapes : Avant de tracer le cercle, on trace les diamètres horizontal et vertical (droites horizontale et verticale passant par le centre) ; ce sont les « traits d'axe du cercle ». Ainsi, lorsque l'on trace le cercle, celui-ci est séparé en 4 quartiers. Pour le séparer en 12 parts égales, on place la pointe du compas sur l'intersection d'un axe et du cercle, tout en gardant un écartement égal au rayon. Puis, on trace les arcs de cercle coupant le cercle. On procède ainsi pour chaque intersection axe-cercle, on obtient au total 12 parts égales.
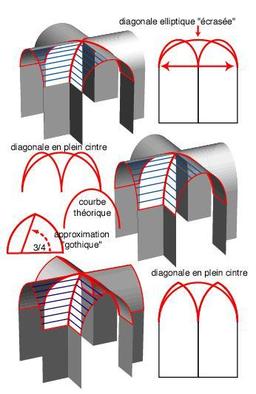
Croisée d'ogives
Genèse de la croisée d'ogives. La projection orthogonale de cette croisée selon l’axe de chacune des nefs donne une demi-ellipse posée dans sa hauteur, très résistante en son sommet. Par chance, il existe une bonne approximation de cet arc pour cette époque où, sur le chantier, à défaut de bons moyens de calcul et de mesures précises il vaut mieux recourir à des tracés simples à exécuter : il s’agit d'un arc brisé composé de deux arcs de cercle centrés respectivement au premier et au troisième quart de la distance à franchir. Cette approximation est souvent observable à une légère déformation de la voûte de la croisée à l'endroit où elle se raccorde aux nefs.
Droite d'Euler
En géométrie euclidienne, dans un triangle non équilatéral, l'orthocentre H, le centre de gravité ou isobarycentre G et le centre du cercle circonscrit \Omega sont alignés et ne sont pas confondus. On appelle droite d'Euler la droite passant par ces trois points. Traduction en français Christophe Catarina.
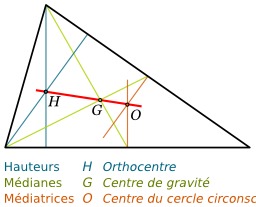
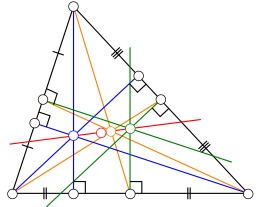
Droite d'Euler dans un triangle
En bleu : les hauteurs ; en orange : les médianes ; en vert : les médiatrices ; en rouge : la droite d'Euler. En géométrie euclidienne, dans un triangle non équilatéral, l'orthocentre H, le centre de gravité ou isobarycentre G et le centre du cercle circonscrit Omega sont alignés et ne sont pas confondus. On appelle droite d'Euler la droite passant par ces trois points.
Dessins et plans, Cercles, Polygones, Aires (surfaces), Aires (surfaces) -- Mesure, Géométrie des nombres, Nombres transcendants, Pi (le nombre)
Encadrement de PI par Liu Hui
Représentation de l'encadrement de π par Liu Hui. Si les calculs pratiques peuvent se faire avec une bonne précision en utilisant la valeur 3,14 comme approximation de π, la curiosité des mathématiciens les pousse à déterminer ce nombre avec plus de précision. Au IIIe siècle, en Chine, Liu Hui, commentateur des Neuf chapitres, propose comme rapport entre le périmètre et le diamètre la valeur pratique de 3 mais développe des calculs proches de ceux d’Archimède mais plus performants et fournit une approximation de π de 3,1416.
Dessins et plans, Géométrie, Cercles, Automobiles -- Essuie-glace, Essuie-glace, Automobiles -- Pare-brise, Technologie
Essuie-glace antagoniste
Essuie-glace à disposition centrée-symétrique ou antagoniste : essuyage opposé.
Dessins et plans, Géométrie, Cercles, Automobiles -- Essuie-glace, Essuie-glace, Automobiles -- Pare-brise, Technologie
Essuie-glace inversé
Essuie glace antagoniste inversé, placé au repos dans l'habillage de chaque pilier du pare-brise.
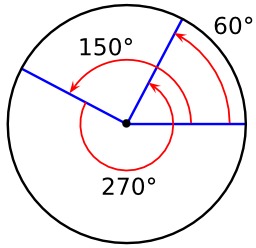
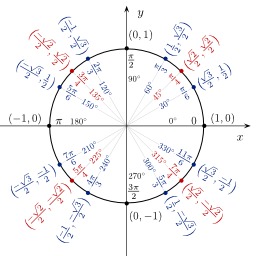
Fonctions trigonométriques dans le cercle unité
Représentation des fonctions trigonométriques dans le cercle unité. Le cercle trigonométrique, en revanche, permet la définition des fonctions trigonométriques pour tous les réels positifs ou négatifs, pas seulement pour des angles de mesure en radians comprise entre 0 et π/2. Sur ce cercle sont représentés certains angles communs, et sont indiquées leurs mesures en radians figurant dans l'intervalle [–2π, 2π], soit deux mesures par angle et même trois pour l'angle nul. Notez que les angles positifs sont dans le sens trigonométrique, contraire à celui des aiguilles d'une horloge, et les angles négatifs dans le sens horaire. Une demi-droite qui fait un angle θ avec la demi-droite positive Ox de l'axe des abscisses coupe le cercle en un point de coordonnées (cos θ, sin θ). Géométriquement, cela provient du fait que l'hypoténuse du triangle rectangle ayant pour sommets les points de coordonnées (0, 0), (cos θ, 0) et (cos θ, sin θ) est égale au rayon du cercle donc à 1. Le cercle unité peut être considéré comme une façon de regarder un nombre infini de triangles obtenus en changeant les longueurs des côtés opposés et adjacents mais en gardant la longueur de leur hypoténuse égale à 1. Source : http://fr.wikipedia.org/wiki/Fonction_trigonom%C3%A9trique.
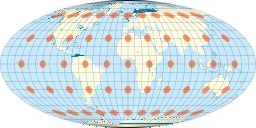
Indicatrices de Tissot sur le planisphère de Mollweide
Indicatrices de Tissot sur le planisphère de Mollweide. Chaque cercle rouge a un rayon de 500 km. Échelle : 1:5,000,000. La projection de Mollweide est une projection cartographique pseudo-cylindrique employée le plus souvent pour les planisphères de la Terre (ou du ciel). Connue aussi sous le nom de projection de Babinet ou projection elliptique, le qualificatif de projection équivalente de Mollweide indique qu'elle privilégie la conservation des surfaces à la conservation des angles (projection conforme) : c'est pourquoi on y recourt principalement pour les cartes de l'ensemble de la sphère reproduites sur une surface réduite. Cette projection fut publiée pour la première fois en 1805 par le mathématicien et astronome prussien Karl (ou Carl) Brandan Mollweide (1774 – 1825) de Leipzig, en tant qu’alternative à la projection de Mercator. Jacques Babinet en vulgarisa l’emploi en 1857, sous le nom de projection homolographique.
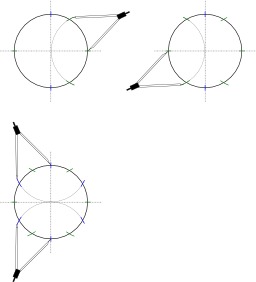
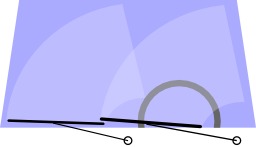
Intersection d'une droite et d'un cercle au compas
Construction au compas seul de l'intersection d'un cercle avec son diamètre : Si la droite (AB) est un diamètre du cercle, et si le point D n'est pas situé sur (AB). On construit de symétrique de D par rapport à (AB). Les deux points à chercher sont les milieux des deux arcs d'extrémités DD'.
Intersection de deux droites
Construction au compas seul de l'intersection de deux droites (étape 1) : construction du point C' symétrique de C par rapport à (AB) et du point E sur (CD) tel que C'C=C'E.
Gravure, Art médiéval, Métaphore, Miniaturistes, Douzième siècle, Latin (langue), Philosophie, Manuscrits à enluminures, Allégories -- Dans l'art, Miniatures (enluminure des livres), Philosophie néoplatonicienne, Sept arts libéraux
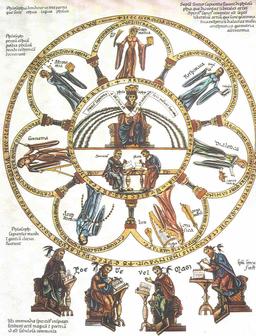
La philosophie et les sept arts libéraux
Représentation de la philosophie et des arts libéraux, in "Hortus Deliciarum" de Herrad von Landsberg, aux alentours de 1180. La philosophie, figure principale, est surmontée de trois têtes identifiées comme étant l'Éthique, la Logique et la Physique. Elle tient dans la main droite une inscription où l'on peut lire "Omnis sapientia a Domino Deo est" (Toute sagesse vient du seigneur), phrase par laquelle débute le texte biblique de l'Ecclésiaste. Sept fontaines de sagesse s'en écoulent, correspondant aux allégories des sept arts libéraux : Grammaire, Rhétorique, Dialectique, Musique, Arithmétique, Géométrie et Astronomie. Dans le cercle central, se trouvent intégrés Socrate et Platon. À l'extérieur, placés au bas de l'image, quatre personnages sont en train d'écrire, chacun étant accompagné d'un oiseau noir perché sur l'épaule qui semble lui chuchoter à l'oreille. Il s'agit d'une allégorie de l'esprit mauvais qui inspire les écrits des auteurs païens. Source : http://fr.wikipedia.org/wiki/Hortus_deliciarum.
Dessins et plans, Géométrie, Ellipses (mathématiques), Cercles, Sections coniques, Hyperboles (mathématiques), Paraboles (mathématiques)
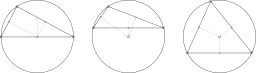
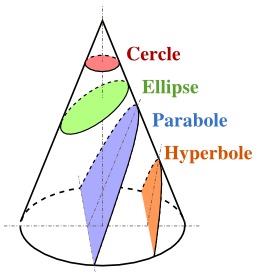
Les quatre sections coniques
Les quatre sections coniques : cercle, ellipse, parabole, hyperbole. Traduction en français Christophe Carina.
Mandala de Sable 03
Premier jour de la réalisation d'un mandala de sable "Pour la paix dans le monde", par trois lamas du temple des Mille Bouddhas, à la Tour de la Liberté de Saint-Dié-des-Vosges, les 11, 12 et 13 avril 2008 : le carré et ses quatre portes, le cercle central.
Mandala de Vajradhatu
Mandala de Vajradhatu (boudhisme tibétain) du XIXème siècle : forme de base carrée avec quatre portes d'entrée, contenant un cercle et un centre (symétrie centrale).
Mesure d'un tour de roue
Relation entre la rotation d'une roue et l'avance d'un véhicule : longueur de l'arc de cercle. En un tour de roue, on avance d'une longueur correspondant au périmètre.
Photographie, Poisson, Poissons de mer, Biologie marine, Poissons, Gymnothorax, Murène javanaise, Mer Rouge, Poissons des récifs coralliens, Poissons des récifs, abcd-six-minutes-pour-la-mer-rouge, Gymnothorax javanicus
Murène javanaise
Gymnothorax javanicus, Communément nommée murène javanaise ou murène géante, est une espèce de poisson de la famille des Muraenidae. De par son importante masse corporelle, elle est la plus grosse espèce de murène. Sa taille peut atteindre une longueur maximale de 300 cm pour 30 kg, cependant les spécimens habituellement rencontrés sont beaucoup plus petits. Son corps serpentiforme possède une teinte de fond brune avec de nombreuses taches sombres à géométrie variable. Les ouvertures branchiales sont cerclées de noir. Source: https://fr.wikipedia.org/wiki/Gymnothorax_javanicus
Photographie, Poisson, Poissons de mer, Biologie marine, Poissons, Gymnothorax, Murène javanaise, Mer Rouge, Poissons des récifs coralliens, Poissons des récifs, abcd-six-minutes-pour-la-mer-rouge, Gymnothorax javanicus
Murène javanaise
Gymnothorax javanicus, communément nommée murène javanaise ou murène géante, est une espèce de poisson de la famille des Muraenidae. De par son importante masse corporelle, elle est la plus grosse espèce de murène. Sa taille peut atteindre une longueur maximale de 300 cm pour 30 kg, cependant les spécimens habituellement rencontrés sont beaucoup plus petits. Son corps serpentiforme possède une teinte de fond brune avec de nombreuses taches sombres à géométrie variable. Les ouvertures branchiales sont cerclées de noir. Source: https://fr.wikipedia.org/wiki/Gymnothorax_javanicus
Photographie, Poisson, Poissons de mer, Biologie marine, Poissons, Gymnothorax, Murène javanaise, Mer Rouge, Poissons des récifs coralliens, Poissons des récifs, abcd-six-minutes-pour-la-mer-rouge, Gymnothorax javanicus
Murène javanaise
Gymnothorax javanicus, communément nommée murène javanaise ou murène géante, est une espèce de poisson de la famille des Muraenidae. De par son importante masse corporelle, elle est la plus grosse espèce de murène. Sa taille peut atteindre une longueur maximale de 300 cm pour 30 kg, cependant les spécimens habituellement rencontrés sont beaucoup plus petits. Son corps serpentiforme possède une teinte de fond brune avec de nombreuses taches sombres à géométrie variable. Les ouvertures branchiales sont cerclées de noir. Source: https://fr.wikipedia.org/wiki/Gymnothorax_javanicus
Photographie, Poisson, Poissons de mer, Biologie marine, Poissons, Gymnothorax, Murène javanaise, Mer Rouge, Poissons des récifs coralliens, Poissons des récifs, abcd-six-minutes-pour-la-mer-rouge, Gymnothorax javanicus, Muraenidae
Murène javanaise
Gymnothorax javanicus, communément nommée murène javanaise ou murène géante, est une espèce de poisson de la famille des Muraenidae. De par son importante masse corporelle, elle est la plus grosse espèce de murène. Sa taille peut atteindre une longueur maximale de 300 cm pour 30 kg, cependant les spécimens habituellement rencontrés sont beaucoup plus petits. Son corps serpentiforme possède une teinte de fond brune avec de nombreuses taches sombres à géométrie variable. Les ouvertures branchiales sont cerclées de noir. Source: https://fr.wikipedia.org/wiki/Gymnothorax_javanicus
Dessins et plans, Géométrie, Cercles, Cercles du triangle, Points (géométrie), Puissances, Puissances (algèbre)
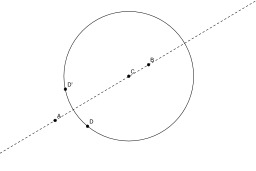
Puissance d'un point
En géométrie euclidienne du plan, la puissance d'un point P par rapport à un cercle de centre O et de rayon R est un nombre qui indique la position de P par rapport à ce cercle.
Dessins et plans, Géométrie, Cercles, Cercles du triangle, Points (géométrie), Puissances, Puissances (algèbre)
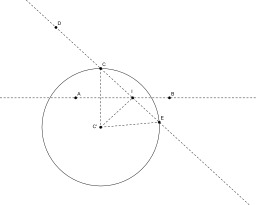
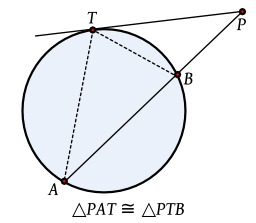
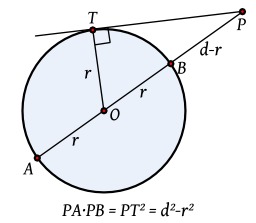
Puissance d'un point
Détermination de la valeur algébrique de la puissance d'un point extérieur à un cercle. En géométrie euclidienne du plan, la puissance d'un point P par rapport à un cercle de centre O et de rayon R est un nombre qui indique la position de P par rapport à ce cercle.
Dessins et plans, Géométrie, Cercles, Cercles du triangle, Points (géométrie), Puissances, Puissances (algèbre)
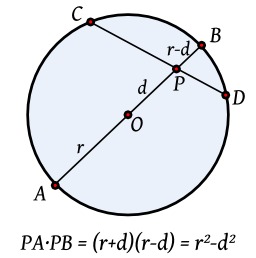
Puissance d'un point intérieur à un cercle
Détermination de la valeur algébrique de la puissance d'un point intérieur à un cercle : PAxPB = (r+d) (r-d).
Quarante-et-un points violets en cercles
Quarante-et-un points violets en trois cercles concentriques autour d'un point central : petit cercle de huit points et deux grands cercles de seize points.
Quart de cercle ayant servi à mesurer la distance à la Lune
Quart de cercle, par Jonathan Sisson, 1742. Monument Historique (Université Claude-Bernard Lyon 1 (Observatoire astronomique de Saint-Genis-Laval), exposé au Musée gallo-romain de Fourvière à Lyon. Utilisé par Jérôme de La Lande pour mesurer la distance entre la Terre et la Lune en 1751.